I. FEJEZET

A VORONOI-DIAGRAM

 

1.§ Voronoi-diagramok értelmezése.

 Fontosabb tulajdonságok

 

            A Voronoi diagram bevezetésénél használjuk a távolság fogalmát. Ebben a dolgozatban az euklideszi távolsággal fogunk dolgozni. Jelöljük a p(px,py) és q(qx, qy) pontok közti euklideszi távolságot d(p, q)-val. Ekkor d(p, q)=.

            1.1 Értelmezés. Legyen P = {p1, p2 ,…, pn} n különböző síkbeli pontot tartalmazó halmaz. A P Voronoi diagramját úgy értelmezzük, mint a sík n cellára (tartományra) való felosztását, azzal a tulajdonsággal, hogy egy q pont a pi ponthoz tartozó cellához tartozik akkor és csakis akkor, ha d(q, pi)< d(q, pj), bármely pjP, j ≠ iesetén.

            A P Voronoi diagramjának jelölése: Vor(P).

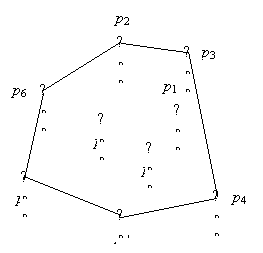
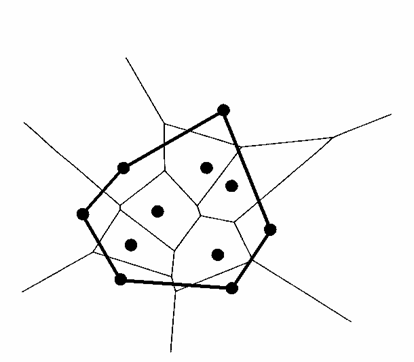
            A pi ponthoz tartozó cellát pedig V(i)-vel jelöljük és a pi Voronoi cellájának nevezzük. Ennek a cellának a Voronoi diagram értelmezése alapján az a tulajdonsága van, hogy a belsejében levő pontok a P pontjai közül a pi-hez vannak a legközelebb.

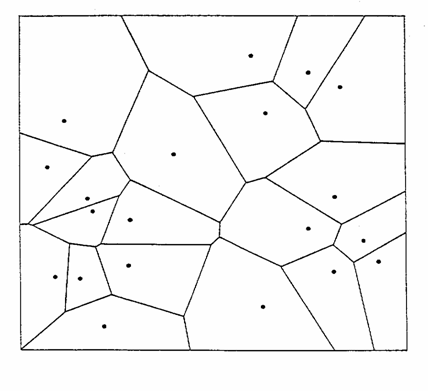
1.1 ábra. Egy 20 pontból álló halmaz Voronoi diagramja

 

            Tekintsük most közelebbről a Voronoi diagramot. Először tanulmányozzuk egyetlen Voronoi cella szerkezetét. Ehhez szükségünk van az alábbi értelmezésre.

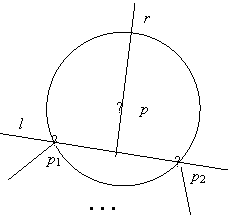
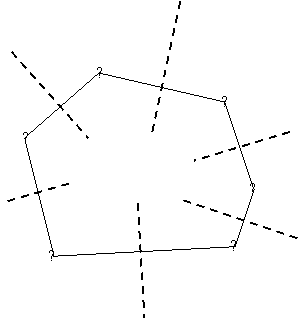
1.2 Értelmezés. Két síkbeli p és q pontok felezőjén a [pq] szakasz felezőmerőlegesét értjük.

            Ez a felező a síkot két félsíkra osztja. A p pontot tartalmazó nyílt félsíkot h(p,q)-val jelöljük, a q pontot tartalmazó nyílt félsíkot pedig h(q, p)-vel. Észrevehetjük, hogy egy r pont akkor és csakis akkor van a h(p,q) félsíkban, ha d(r, p) < d(r, q). Innen azonnal kapjuk az alábbi megjegyzést.

            1.1 Megjegyzés. .

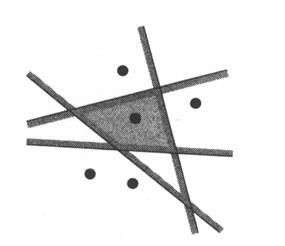
1.2. ábra. Egy pont Voronoi-cellája

 

            Tehát a V(i) cellát n–1 félsík metszetéből kapjuk és így V(i) egy (megtörténhetik, hogy nem korlátos) nyílt konvex sokszög belső tartománya lesz, amelynek legtöbb n–1 éle és n–1 csúcsa van.

            Hogyan nézhet ki tehát egy Voronoi diagram? Azt már láttuk, hogy minden cella bizonyos számú félsík metszete és így a Voronoi diagram tényleg a sík egy felosztása lesz, amelynek élei szakaszok vagy félegyenesek. Teljes egyenes csak akkor lehet él, ha minden pont kollineáris.

            1.1 Tétel. Legyen P n síkbeli pontot tartalmazó halmaz. Ha az összes pont kollineáris, akkor a Vor(P) n–1 párhuzamos egyenesből áll. Különben  Vor(P) összefüggő és az élei vagy szakaszok, vagy félegyenesek (lásd 1.1 ábra).

            Bizonyítás. A tétel első részének a bizonyítása azonnali, így feltételezzük, hogy nem minden pont kollineáris a P-ben.

            Először igazoljuk, hogy a Vor(P) élei vagy szakaszok, vagy félegyenesek. Azt már tudjuk, hogy a diagram élei a pontpárok felezőinek (tehát egyeneseknek) részei. Tételezzük, fel, hogy mégis létezik egy e él a Vor(P)-ben, amely egy teljes egyenes.

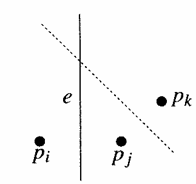
1.3. ábra. Az e él a pi és pj pontok felezőmerőlegesének része.

 

 Legyen e a V(i) illetve a V(j) cellákat határoló egyenes. Legyen pkP egy pont, amely nem kollineáris a pi és pj pontokkal. Így a pj és pk felezője nem lesz párhuzamos az e-vel és ezért metszeni fogja azt. De az e egyenes azon része, amely a h(pk, pj) belsejében van nem lehet a V(j) határán, mert közelebb van a pk-hoz, mint a pj ponthoz. Tehát ellentmondáshoz jutottunk.

            Még azt kell belátnunk, hogy a Vor(P) összefüggő. Ha ez nem lenne igaz, akkor létezne egy V(i) Voronoi cella, amely a síkot kétfelé osztja. De mivel a Voronoi cellák konvexek, a V(i) két párhuzamos egyenes által határolt tartomány lenne. De épp az előbb igazoltuk, hogy a Voronoi diagram élei nem lehetnek egyenesek. Ezzel ellentmondáshoz jutottunk és a tételt teljesen igazoltuk. □

            A továbbiakban végig az alábbi fontos feltételezés mellett dolgozunk:

            Feltételezés. A P bármely 4 pontja nem helyezkedik el ugyanazon a körön.

Ezzel a feltételezéssel a Voronoi diagram szerkezete leegyszerűsödik.

            1.2 Tétel. A Voronoi diagram bármely csúcsából pontosan három él indul ki, vagyis a Voronoi csúcs foka pontosan három.

            Bizonyítás. Bármely Voronoi csúcs bizonyos számú Voronoi él metszete. Legyenek e1, e2, …, ek azon Voronoi élek, amelyek metszéspontja a v Voronoi csúcs, az ei él közös éle a V(i–1) és  V(i) Voronoi celláknak minden i = 2,3, …,k esetén és e1 a V(k) és V(1) cellák közös éle.

 

 

 

 

 

 


                                                                      

 

 

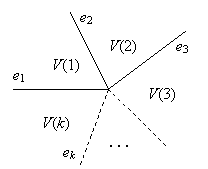
1.4 ábra Egy Voronoi-csúcs és az itt találkozó Voronoi-élek

           

            Mivel a v Voronoi csúcs rajta van az e1 élen, a v egyenlő távolságra van a p1 és pk pontoktól. Hasonlóan, mivel vei, (i =2,…,k) következik, hogy a v egyenlő távolságra van a pi-1 és a pi pontoktól is. Tehát v ugyanakkora távolságra van az összes pi (i = 1,…k) pontoktól. Ez azt jelenti, hogy az összes ilyen pi (i = 1,…k) rajta van a v középpontú és [vpi] sugarú körön. De feltételeztük, hogy bármely négy pont nem lehet egy körön, következik, hogy k3.

            Ha k=2, akkor az e1 és e2 élek a v(1) és v(2) Voronoi cellák közös élei. Így mindkettő a p1 és p2 felezőjéhez tartoznak és ezért a v csúcs tulajdonképpen valamely Voronoi él belső pontja, tehát nem lehet egy Voronoi csúcs. Ez ellentmondás.

            Ha k=1, akkor az e1 él mindkét oldalánál ugyanaz a v(1) Voronoi cella van. Tehát a Voronoi cella nem konvex, amely megint ellentmondás.

            Tehát a k pontosan egyenlő hárommal. □

            1.2 Megjegyzés. Az 1.2 Tétel bizonyításából kiderül, hogy a Voronoi csúcsok az eredeti ponthalmaz három pontja meghatározott körök középpontjai. Egy v csúcs esetén ezt a kört C(v)-vel jelöljük. Ezek a körök az alábbi érdekes tulajdonságokkal rendelkeznek:

            1.3 Tétel. A P Voronoi diagramjának bármely v Voronoi csúcsa  esetén a C(v) kör nem tartalmaz a belsejében más pontot P-ből.

            Bizonyítás. Legyen például pi, pj, pk három pont a P halmazból, amelyek meghatározzák a C(v) kört (lásd 1.5 ábra). Ekkor a C(v) kör értelmezése alapján v a V(i), V(j), V(k) Voronoi-cellák határán van.

 

 

 

 

 

 

 

 

 

 

 

 

 

 


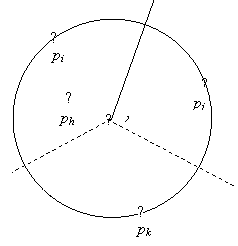
1.5. ábra A pi, pj, pk pontok által meghatározott C(v) kör

 

            A Voronoi-cellák értelmezését felhasználva belátható, hogy pi, pj és pk a v csúcshoz legközelebbi pontok.

            Feltételezzük, hogy létezik egy pkP pont a C(v) kör belsejében. Ekkor a v közelebb lenne a pk ponthoz, mint a pi, pj és pk pontokhoz, vagyis a v a V(k)-ban lenne, nem pedig a V(i), V(j) vagy V(k)-ban. Ezzel ellentmondáshoz jutottunk. □

            Tételezzük fel, hogy megszerkesztettük a Voronoi-diagramját az n pontból álló P halmaznak. Az alábbi tétel kimondja, hogy bármely piP esetén a pi-hez legközelebbi P-beli pontot megtalálhatjuk „lokálisan” nézve a V(i) Voronoi-cellát.

            1.4 Tétel.  A P tetszőlegesen adott pi pontjának a legközelebbi szomszédja meghatároz egy élet a V(i) Voronoi-cellában.

            Bizonyítás. Legyen pj a pi-hez legközelebbi pont és v a pipj szakasz felezőpontja. Tekintsük a pi középpontú és [piv] sugarú   C kört.

            Először igazoljuk, hogy a C kör teljesen a V(i) Voronoi-cella belsejében van. Tételezzük fel az ellemkezőjét. Ekkor létezne a V(i) Voronoi-cellának egy e éle, amely tartalmaz egy n pontot a C kör belsejében (lásd 1.6 ábra). Ekkor e a [pipk] szakasz  felezőmerőlegesén helyezkedik el, ahol pkP, kj.

Így [pi pk]2[piu]<2[piv]=[pipj]. Tehát a pi pont közelebb van a pk-hoz, mint a pj-hez ellentmondva annak a feltételnek, hogy pj a pi-hez legközelebbi pont.

Tehát a C kör teljesen a V(i) Voronoi-cella belsejében van. Mivel a [vpj] szakasz minden pontja közelebb van a pj-hez, mint a pi-hez és a vC, következik, hogy a v rajta van a V(i) cella határán.

 

 

 

 

 

 

 

 


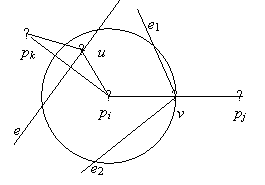
1.6 ábra.

 

            A továbbiakban igazoljuk, hogy a v belső pontja a V(i) határán levő valamely élnek. Tételezzük fel az ellenkezőjét, vagyis azt, hogy v egy Voronoi-csúcs. Legyen e1 és e2 két él a V(i) cella határán, amelyek a v-ben metszik egymást. Mivel V(i) konvex, az e1ve2 szög mértéke kisebb mint 180 fok (lásd 1.6 ábra). De legalább az egyik él metszeni fogja ekkor a kört. Ez pedig lehetetlen az előbbiek alapján.

            Tehát létezik egyetlenegy e1 Voronoi-éle a V(i) cellának, amely tartalmazza a v-t. Ez az e1 él érintője kell legyen a C körnek, különben metszené azt. Így az  e1 él része a [pipj] szakasz felezőmerőlegesének, vagyis az e1 élet a pj pont határozza meg. □

            A Voronoi-diagramok szerkezetének vizsgálata után tanulmányozzuk a diagram komplexitását, vagyis az éleinek és csúcsainak számát. Mivel n pontunk van és minden pont Voronoi-cellájának legtöbb n-1 oldala van, azt mondhatjuk, hogy a komplexitás legfennebb kvadratikus. Feltevődik a kérdés, hogy megtörténhet-e az, hogy egy cellának lineáris a komplexitása, egy másiknak pedig kvadratikus komplexitása legyen. A választ az alábbi tétel adja és tagadja ezt.

            1.5 Tétel. Egy n síkbeli pontból álló halmaz Voronoi diagramjában a csúcsok száma legtöbb 2n-5 és az élek száma legtöbb 3n-6.

            Bizonyítás. Ha a pontok kollineárisak, akkor a tétel azonnal következik az 1.1 Tételből, tehát most feltételezzük, hogy most ez nem áll fenn.

            A tétel bizonyításához felhasználjuk az Euler képletet, amely azt mondja ki, hogy segy összefüggő síkbeli mcs csúccsal, me éllel és mc „cellával” rendelkező gráf esetén az mcs-me+mc=2 összefüggés áll fenn.

            Ezt a képletet direkt nem alkalmazhatjuk a Vor(P) diagramra, mert a Vor(P)-nek vannak félegyenes élei, tehát nem igazi gráf. Hogy ezt kikerüljük bevezetünk egy plussz V() csúcsot a „végtelenben” és a Vor(P) félegyenes éleit úgy tekintjük, hogy átmennek ezen a plusz ponton. Így egy összefüggő síkbeli gráfot kapunk (lásd 1.7 ábra)

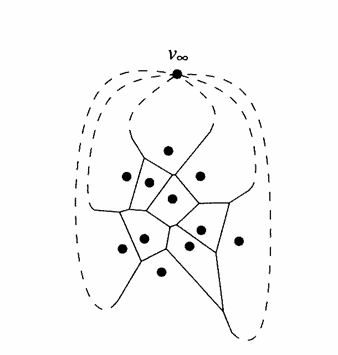
1.7 ábra. A Voronoi-diagram a  csúccsal

 

            Jelölje a Vor(P) csúcsok számát: ncs+1 (csúcsok száma és a plusz V() csúcs), az éleinek számát ne; n a cellák száma. Ekkor alkalmazva Euler képletét kapjuk, hogy:

            (1.1)                (ncs+1)-ne+n=2,

vagyis

            (1.2)                ncs-ne=1-n.

            Ezenkívül minden csúcs foka három, kivéve a V() csúcsot, amelynek foka nagyobb mint három és minden élnek két csúcsa van. Ez azt jelenti, hogy:

            (1.3)                2ne=3ncs+.

            Az (1.2) alapján ncs=ne+1-n, ezt behelyettesítve az (1.3)-ba következik, hogy:

2ne=3(ne+1-n)+ne=3n-3-3n-6.

            Most ezt az egyenlőséget és az (1.2)-t felhasználva írhatjuk, hogy:

ncs=ne+1-n3n-6+1-n=2n-5. □

            1.3 Megjegyzés. Egy Voronoi-cellának legtöbb n-1 éle lehet, de az összes élek száma kevesebb vagy egyenlő mint 3n-6. Minden él két cellához tartozik pontosan. Ez azt jelenti, hogy egyenlet Voronoi-cella éleinek átlagszáma nem haladhatja meg a hatot (ha meghaladja vagy egyenlő, akkor 6n6n-12, ami ellentmondás).

            Ezt a paragrafust a Voronoi-diagram éleinek és csúcsainak egy jellemzési tételével fejezzük be. Tudjuk, hogy az élek a pontpárok felezőinek részei és a csúcsok pedig ezen felezők metszéspontjai. A felezők száma kvadratikus, de ugyanakkor a Vor(P) bonyolultsága csak lineáris. Így hát nem minden felező határoz meg élet a Vor(P)-ben és nem minden metszet lesz csúcs. Ahhoz, hogy meghatározzuk, hogy melyik felezők és metszetek határoznak meg Voronoi elemeket bevezetjük a következő értelmezést.

            1.2 Értelmezés. Egy qP pont esetén a q legnagyobb köre P-re vonatkozóan az a legnagyobb kör, amelynek a q a középpontja  és nem tartalmaz egyetlen pontot sem P-ből. A kör jelölése: CP(q).

 

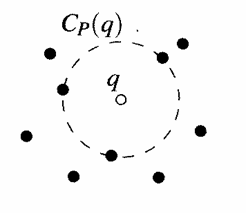
1.8 ábra. A q legnagyobb köre P-re vonatkozóan

 

            1.6 Tétel.(Voronoi élek és csúcsok jellemzési tétele) Egy P ponthalmaz Vor(P) diagramja esetén fennállnak az alábbi tulajdonságok:

            (i) A q pont a Vor(P) egy csúcsa, akkor és csakis akkor, ha a CP(q) legnagyobb kör tartalmaz legalább három pontot P-ből a határán.

            (ii) A pi és pj pontok felezője meghatároz egy élet a Vor(P)-ben akkor és csakis akkor, ha létezik egy q pont a síkban úgy, hogy CP(q) tartalmazza a pi és pj pontokat a határán, de egyetlen más P-beli pontot sem.

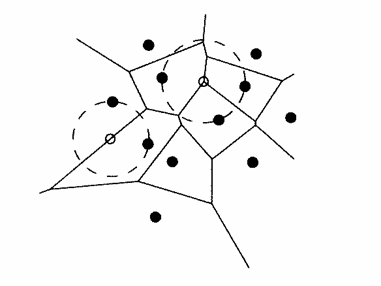
1.9 ábra.

 

            Bizonyítás. (i) Tételezzük fel, hogy létezik egy q pont úgy, hogy CP(q) tartalmaz legalább három P-beli pontot a határán. Legyen ezek közül három: pi, pj és pk. Mivel intCP(q)=0 kapjuk, hogy q a V(i), V(j) és V(k) cellák határán kell legyen, vagyis q egy csúcs Vor(P)-ben.

            Visszafelé, minden qVor(P) csúcs legalább három Voronoi él találkozásának felel meg. Az ezeknek megfelelő  Voronoi cellák közül három legyen például V(i), V(j) és V(k). A q csúcs egyenlő távolságra van ekkor a pi, pj és pk pontoktól és nem lehet más pont közelebb q-hoz, különben z V(i), V(j) és V(k) cellák nem találkoznak a q-ban. Tehát az a kör, amelynek q a középpontja és tartalmazza a pi, pj és pk pontokat nem tartalmaz más P-beli pontot.

            (ii) Tételezzük fel, hogy létezik egy q pont a tételbeli tulajdonságokkal. Mivel intCP(q) nem tartalmaz pontot P-ből és pi, pj a CP(q) határán vannak, kapjuk, hogy d(q,pi)=d(q,pj)d(q,pk) . Következik, hogy q vagy egy élen van a Vor(P)-ben, vagy q egy csúcs. A tétel (i)-k pontja alapján viszont q nem lehet csúcs. Tehát q egy élen található a Vor(P)-ben, amely élet a pi és pj felezője határozza meg.

            Fordítva, tételezzük fel, hogy a pi és pj pontok felezője meghatároz egy élet Vor(P)-ben. Ekkor az él bármely belső q pontjának a legnagyobb CP(q) köre fogja a körön tartalmazni a pi és pj pontokat, de ezeken kívül egyet sem. □

 

2.§ A Voronoi-diagramok és konvex

burkolók kapcsolata

 

            2.1 Értelmezés. A sík egy P részhalmazának konvex halmaznak nevezzük, ha bármely p,qP pontok esetén a [pq] szakasz teljes egészében a P halmazban van.

            2.2 Értelmezés. A P halmaz konvex burkolója (jel. CH(P) a jelölés a „convex hull of P = P konvex burkolója elnevezésből ered) a legkisebb konvex halmaz, amely tartalmazza a P-t, pontosabban, olyan konvex halmaz metszete, amelyek tartalmazzák a P halmazt.

            Például, ha P={p1,p2,…,p9}, akkor a P konvex burkolóját az alábbi ábra szemlélteti:

 

 

 

 

 

 

 

 

 

2.1 ábra.

 

            A továbbiakban vizsgáljuk a konvex burkoló és a Voronoi-diagram kapcsolatát.

            Legyen r egy félegyenes, amelynek a p0 a kezdőpontja. Bármely pr esetén jelöljük rp-vel azt a félegyenest, amelyet az r félegyenesből kapunk levágva belőle a p0p szakaszt.

            2.1 Tétel. Két pont a P halmazból a CH(P) konvex burkoló két egymást követő pontja, akkor és csakis akkor, ha a nekik megfelelő Voronoi-celláknak van egy közös élük, amely egy félegyenes.

            Bizonyítás. Legyen p1 és p2 két pont a P-ből és legyen V(1) és V(2) a nekik megfelelő Voronoi-cella Vor(P)-ből.

            „” Tételezzük fel, hogy a p1 és p2 pontok a CH(P) konvex burkoló egymást kívető csúcsai. Ekkor a p1p2 szakasz a CH(P) konvex burkoló határán egy él lesz. Legyen l a p1p2 szakasz tartóegyenese (az az egyenes, amely tartalmazza a p1p2 szakaszt). Ekkor a konvex burkoló egy ismert tulajdonsága alapján az L egyenes egyik oldalán van a P összes pontja és a másik oldalon nincs egyetlen pont sem. Legyen r egy félegyenes, amely a p1p2 szakasz felezőpontjából indul ki, merőlegesen erre a szakaszra és az l egyenes által meghatározott azon félsíkban van, amely nem tartalmaz P-beli pontokat.

 

 

 

 

 

 

 

 

 

 


2.2 ábra

 

Legyen pr egy pont és Cp egy p középpontú pp1 sugarú kör. Ahogy a p pont távolodik az l egyenestől úgy a p1p2 körív mind jobban közeledik az l egyeneshez ( a p1p2 szakaszhoz). Mivel a P halmaz egyetlen pontot sem tartalmaz, amely az l egyenes ugyanazon az oldalán lenne mint a p, a P halmaz véges számú pontot tartalmaz. Következik, hogy léteznie kell egy p0r pontnak úgy, hogy a P\{p1,p2} halmaz egyetlen pontja sincs a Cp körben, bármely p pontra, amely a p0 pont mögött van. Ekkor bármely p esetén p közelebb van a p1, p2 pontokhoz, mint a P\{p1,p2} bármely pontjához.  Tehát  egy Voronoi-élen kell legyen, amely határolja a V(1) és V(2) cellákat, vagyis a V(1) és V(2) celláknak van egy közös élük, amely egy félegyenes.

            „” Feltételezzük, hogy a V(1) és V(2) celláknak van egy közös élük, amely egy  r félegyenes. Ekkor az  r bármely p pontja közelebb van p1p2 szakaszhoz, mint a P összes többi pontjához és egyenlő távolságra van a p1,p2 pontoktól. Legyen Cp egy kör, amelynek egy pr a középpontja és átmegy a p1 és p2 pontokon. Ekkor az r félegyenes bármely pr esetén az intCp nem tartalmaz más pontot a P-ből. Ha a p pont távolodik az r félegyenesen a végtelen felé, akkor a p1p2 körív mind közelebb kerül a p1p2 szakasz l tartóegyeneséhez és nem tartalmaz P-beli pontot. Mivel P véges, levonhatjuk a következtetést, hogy az l egyenes egyik oldalán nincsenek P-beli pontok. Ez azt jelenti, hogy p1p2 a CH(P) konvex burkoló határán, egy élen található. Tehát p1p2 a CH(P) konvex burkoló két egymás melletti csúcsa. □

            2.1 Következmény. A Vor(P) diagram egy V(i) cellája nem korlátos akkor és csakis akkor, ha a neki megfelelő pont a P halmazból a CH(P) konvex burkoló egy csúcsa.

            Bizonyítás. A CH(P) konvex burkoló bármely p csúcsának van egy p’ szomszédja (a p mellette csúcs). Ekkor a 2.1 Tétel alapján a V illetve V’ Voronoi-celláknak van egy közös élük, amely egy félegyenes. Tehát a V cella nem lehet korlátos.

            Visszafelé, ha egy V Voronoi-cella nem korlátos, akkor a V-nek kell legyen egy félegyenes éle, amely közös egy másik V’ cellával. Újra felhasználva a 2.1 Tételt következik, hogy a megfelelő p és q pontok a CH(P) konvex burkoló egymás melletti csúcsai. Tehát a V Voronoi-cellának megfelelő p pont a konvex burkoló egy csúcsa. □

            2.1 Megjegyzések. a) Az előző tétel és következmény alapján, ha már megszerkesztettük a Vor(P) diagramot, akkor innen azonnal megkapjuk a CH(P) konvex burkolót. Egyszerűen megkeressük azokat a Voronoi éleket, amelyek félegyenesek, utána megkeressük azokat a pontokat a P-ből, amelynek Voronoi-cellái tartalmazzák ezeket a félegyenes éleket és összekötjük őket (mindeniket a hozzá legközelebbivel).

2.3 ábra. A Voronoi-diagram és a konvex burkoló

            b) Ha pedig megszerkesztettük először a CH(P) konvex burkolót, akkor a Voronoi diagram félegyenes éleiről elmondhatjuk, hogy a konvex burkolót határoló élek felezőmerő­legesein vannak.

 

 

 

 

 

 

 

 

 

 

 

 

 

 


2.4 ábra. A konvex burkoló és a Voronoi-diagram félegyenes élei

           

            A dolgozatunkban mi egy olyan algoritmust adunk a Voronoi-diagram megszer­kesztésére, amelyben használjuk a konvex burkolókat. A konvex burkolók megszerkesztésére számos algoritmust írtak. Ezek közül az egyik legismertebb az „oszt meg és uralkodj” programozási módszert használó algoritmus. Mi is ezt a módszert használjuk a Voronoi-diagram megszerkesztéséhez és felhasználjuk benne a konvex burkolók meghatározásához szükséges úgynevezett „alsó” és „felső híd” fogalmát. Ezért itt megadjuk értelmezésüket és a meghatározási módjukat.

            Először is a konvex burkolók meghatározása úgy történik, hogy két részre osztjuk a pontok S halmazát és mindkét részhalmazra újra meghívjuk a konvex burkolót meghatározó algoritmust. A gond csak ott lesz, amikor a két részhalmaz konvex burkolója (CH(S1) és CH(S2)) ismeretében meg kell határozzuk az egész halmaz konvex burkolóját.  Itt vezették be az „alsó” és „felső híd” fogalmát.

            2.3 Értelmezés. Azt az egyenest, amely érintője a CH(S1) és CH(S2) konvex burkolók­nak felülről (alulról), a CH(S1) és CH(S2) felső (alsó) hídjának nevezzük.(lásd 2.5 ábra)

 

 

 

 

 

 


            A felső híd megkeresése a következőképpen történhet. Kiválasztunk egy tetszőleges p csúcsot a CH(S1)-ből, egy tetszőleges q csúcsot a CH(S2)-ből és legyen l a p és q pontokon áthaladó egyenes. Utána megpróbáljuk „feltolni” ezt az l egyenest úgy, hogy messe a CH(S1) és CH(S2) konvex burkolókat. Amikor már nem tudjuk tovább feltolni, akkor megtaláltuk a felső hidat. Teljesen szimmetrikusan határozhatjuk meg az alsó hidat is.

            Nézzük most ezt leírva algoritmus formájában egy kicsit részletezve:

 

            FELSŐHÍD (CH(S1), CH(S2))

BEMENET: A CH(S1) és CH(S2) konvex burkolók elválasztva egy függőleges egyenessel úgy, hogy CH(S1) az egyenes baloldalán legyen;

                        KIMENET: A CH(S1) és CH(S2) felső hídjaé

                        BEGIN

1.      Legyen p az a pont a CH(S1) burkolóból, amelynek a legkisebb az x koordinátája és q a CH(S2)-ből a legnagyobb x koordinátájú pont. Legyen l egy egyenes a p és q ponton keresztül;

2.      AMÍG (l nem a felső híd) VÉGEZD EL

2.1. AMÍG (létezik egy p1 pont CH(S1)-ben, amely az l egyenes fölött van)

kicseréljük a p és p1 pontokat egymással és megszerkesztjük az új l egyenest;

2.2. AMÍG (létezik egy q1 pont CH(S2)-ben, amely az l egyenes fölött van)

kicseréljük a q és q1 pontokat egymással és megszerkesztjük az új l egyenest;

(AMÍG) vége

                        END.