Feladat:

Adott az S halmaz, amely a sík n pontját tartalmazza. Keressük meg azt a három pontot az S halmazból, amelyek a legkisebb területű háromszöget alkotják.

Naiv megoldás (brute – force) :

A feladat megoldható úgy, hogy minden ponthármas által alkotott háromszög területét kiszámítjuk és ezek közül választjuk ki a legkisebbet. Ennek az algoritmusnak létezik egy gyorsabb változata is, melyben minden p_i p_j pontpárra az S-ből kiszámoljuk a d(k,i,j) távolságot a p_k ponttól a p_i és p_j által meghatározott egyenesig, minden p_k eleme S-{p_i, p_j }-re. Mivel a p_k, p_i és p_j által alkotott háromszög területe egyenlő a d(k,i,j)*|p_ip_j| szorzat felével, így megkapjuk az összes olyan háromszög területét, melynek p_ip_j oldala. Ezt elvégezve minden pontpárra az S-ből, megkapjuk az összes olyan háromszög területét melynek csúcspontjai az S halmazhoz taroznak. Ezekből kell kiválasztanunk a legkisebb területűt. A fenti algoritmus gyorsabb ugyan, de bonyolultság szintén O(n3).

Értelmezés:

Legyen p egy pont és l egy egyenes. A függőleges távolsága p-nek l-től a p pont és a p-ben húzott függőleges egyenes l egyenessel való metszéspontja között lévő távolság. Ezt d_v(p,l)-el jelöljük.

Megjegyzés:

A legtöbb esetben egy pont távolsága egy egyenestől nem esik egybe a pont függőleges távolságával az egyenestől.

Jelölés:

Legyen d_v(k,i,j) a p_k pont függőleges távolsága a p_i és p_j által alkotott egyenestől. Az egyszerűség kedvéért, szintén d_v(k,i,j)-el jelöljük a a p_k pont függőleges távolságát a p_i p_j szakasztól.

1. Lemma:

Rögzítsük a p_i és p_j pontokat az S-ből. Legyen l_i,j a p_i és p_j pontok által meghatározott egyenes. Ekkor egy p_k pont S-{p_i, pipk }-ből legkisebb d(k,i,j) távolságra van l_i,j-től, akkor és csakis akkor ha p_k van a legkisebb d_v(k,i,j) függőleges távolságra l_i,j-től.

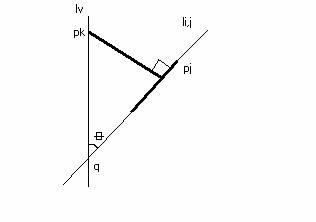
Bizonyítás:

Legyen l_v az a függőleges egyenes, amely áthalad a p_k ponton és metszi az l_i,j egyenest q pontban. Jelölje θ az l_i,j és l_v által alkotott szöget. A d_v(k,i,j) függőleges távolság ekkor egyenlő a p_kq szakasz hosszával és könnyű belátni, hogy hossza ׀p_kq׀*sin θ. Következik, hogy d_v(p_k,l_i,j) és d(p_k,l_i,j) arányosak. Így a lemma nyilvánvalóan igaz.

A legkisebb háromszög megkeresésekor a p_i és p_j S-beli pontpárok esetén csak az olyan p_k pontokat kell tekintenünk, melyek az S-{p_i, p_j }-ből vannak és d_v(k,i,j) a legkisebb.

Először egy T₁ transzformációt hajtunk végre S pontjain. A T₁ egy p_k pontot az S-ből egy T₁(p_k) egyenesbe visz át, míg a p_i-n és p_j-n áthaladó l_i,j egyenest a T₁(l_i,j) pontba, mely egybeesik a T₁(p_i) és T₁(p_j) egyenesek metszéspontjával. Ezen transzformáció egy hasznos tulajdonságát bizonyítjuk a következő lemmában.

2. Lemma:

A függőleges távolsága p_k-nak l_i,j -től d_v(k,i,j) egyenlő a függőleges távolságával T₁(l_i,j)-nek T₁(p_k)-tól d_v(T₁(p_k),T₁(l_i,j)).

d_v(k,i,j)= d_v(T₁(p_k),T₁(l_i,j))

Bizonyítás:

Legyen p_i két koordinátája a_i és b_i, p_j-nek a_j és b_j, p_k-nak a_k és b_k.

Ekkor az l_i,j egyenlete a következő:

A p_i, p_j és p_k pontokat a transzformáció a következő egyenesekké alakítja:

T₁(p_i): y=a_ix+b_i

T₁(p_j): y=a_jx+b_j

T₁(p_k): y=a_kx+b_k

Az l_i,j pont pedig:

Az l_i,j és a p_k-n áthaladó függőleges egyenes metszéspontja:

Ekképpen a p_k függőleges távolsága l_i,j -től a következő szám abszolút értéke lesz:

Hasonlóképpen a T₁(p_k) egyenes és T₁(l_i,j)-n áthaladó függőleges egyenes metszéspontja:

Ugyanakkor a függőleges távolsága T₁(p_k) egyenesnek a T₁(l_i,j) ponttól a következő szám abszolút értéke:

Ez tehát bizonyítja a lemmát.

De miben is segít ez a lemma? Előbb alakítsunk át T₁ transzformációval minden pi pontot az S-ből T₁(p_i) egyenessé, minden i=1,…,n -re. Így egy n darab egyenesből álló halmazt kapunk.

T₁(S)= {T₁(p₁),T₁(p₂),…,T₁(p_n)}

A T₁(S) halmaz, amely n egyenest tartalmaz T₁(p_i), i = 1,…,n, egy síkgráfot alkot, ha minden két vonal metszetét T₁(S)-ből a gráf csúcspontjának tekintjük. Legyen l_i,j a p_i és p_j által meghatározott egyenes S-ben. Ahhoz, hogy megtaláljuk azt a pontot az S-ből, amelynek a legkisebb a függőleges távolsága az li,j egyenestől, minden csúcspontot meg kell vizsgáljunk S-{p_i, p_j }-ből . Ahhoz, hogy megtaláljuk a T₁(p_k) vonalat T₁(S)-ből úgy, hogy a T₁(l_i,j) pontnak legyen a legkisebb függőleges távolsága T₁(p_k)-tól, csak a T₁(S)-ben a rögtön T₁(l_i,j) felett és alatt lévő egyeneseket szükséges ellenőrizni. Ezért, ha megfelelően kezeljük a T₁(S) síkgráfját, hatékonyan tudjuk megtalálni azt a T₁(p_k) egyenest T₁(S)-{T₁(p_i),T₁(p_j)}-ből, melyre a T₁(li,j) ponttól való függőleges távolsága a legkisebb lesz. A két ismertetett lemmából következik, hogy a p_k pont távolsága a legkisebb minden S-{p_i, p_j }pont közül az l_i,j -től, ami miatt a Δ(p_k,p_i,p_j) háromszög a legkisebb területű azok közül, melyeknek egyik éle a p_ip_j szakasz. Minden p_i és p_j pontpárra S halmazból végrehajtjuk a fentieket és megkapjuk a legkisebb területű háromszöget.

Lássuk hogyan kell megkeresni azt az egyenest amely legközelebb van a T₁(l_i,j) ponthoz T₁(S)-ből. Végrehajtunk egy síksöprést a T₁(S) síkgráfján balról jobbra egy L egyenessel. A T₁(S)-beli egyeneseket egy A 2-3 fában tároljuk az L-en való metszéspontjuk szerint rendezve. Mivel T₁(S)-ben pontosan n darab egyenes van az A 2-3 fának n levele van és mélységét O(log n) határolja. Feltételezzük, hogy egy adott pillanatban az L egyenes egy T₁(l_i,j) csomóponton halad át; ekkor könnyű belátni, hogy a T₁(p_i) és T₁(p_j) egyenesek kivételével, melyek T₁(l_i,j)-ben metszik egymást, T₁(S) minden egyenese fenntartja egymással szembeni relatív pozícióját az A 2-3 fában. Másfelől pedig T₁(p_i) és T₁(p_j) egyenesek helyet cserélnek az A 2-3 fában. Másképpen fogalmazva, ha a T₁(p_i) egyenes a T₁(p_j) egyenes fölött található a T₁(l_i,j) pont bal felén, akkor a T₁(p_i) a T₁(p_j) egyenes alatt kell elhelyezkedjen a T₁(l_i,j) pont jobb felén, és fordítva. Legyen a rögtön T₁(l_i,j) csomópont fölött és a rögtön alatta lévő két egyenes az S síkgráfjában T₁(p_k) illetve T₁(p_h). Ekkor T₁(p_k) és T₁(p_h) is O(log n) idő alatt érhető el az A 2-3 fában. Hogy egy T₁(l_i,j) csúcspont relatív helyét az A 2-3 fában megtaláljuk, egy keresést indítunk a fában az y koordináta szerint és közben rögzítjük minden egyenes x koordinátáját A-ban a T₁(l_i,j) x koordináta értékére.

A következő algoritmus a fentiek implementációja egy S halmaz pontjai közül adja meg azt a hármat, amely a legkisebb területű háromszöget alkotja.

Algoritmus LEGKISEBB-HÁROMSZÖG (S)

Adott: egy síkbeli pontokat tartalmazó S halmaz

Eredmény: három pont S-ből, amely a legkisebb háromszöget alkotja

BEGIN

1. Minden pi pontra S-ből, i=1,...,n szerkeszd meg a T₁(p_i) egyenest.

2. Mindegyik első lépésben szerkesztett T₁(p_i) és T₁(p_j) egyenespárra i,j=1,...,n számítsd ki a metszéspontjukat, a T₁(l_i,j) csúcspontot.

3.

Rendezz minden T₁(l_i,j) metszési csúcsot, i,j=1,...,n, x koordináta szerint növekvő sorrendbe. Legyen a rendezett lista {v₁,…,v_m}, ahol

és v_i=(x_i,y_i), i=1,...m.

4. Építsd fel az A 2-3 fát, amelynek levelei a T₁(p_i) egyenesek, i=1,...,n, az x=x1-1 egyenesen való metszéspontjuk y koordinátája szerint rendezve.

5. Minden r=1,...,n esetén végezd el

Feltételezzük, hogy a v_r csúcspont a T₁(p_i) és T₁(p_j) egyenesek metszési csúcsa és a rögtön felette és rögtön alatta lévő egyenesek T₁(p_k) és T₁(p_h). Számítsd ki a Δ(p_k,p_i,p_j) és Δ(p_h,p_i,p_j) háromszögek területét. Cseréld ki a T₁(p_i) és T₁(p_j) egyenesek pozícióját az A 2-3 fában.

6. A háromszög, amelyet az 5. lépésben szerkesztettünk és a területe a legkisebb, lesz a legkisebb területű háromszög.

END

Nem tárgyaltuk azt az esetet mikor három egyenes T₁(p_i), T₁(p_j) és T₁(p_k) egy pontban metszi egymást. Ebben az esetben a T₁(l_i,j) metszéspontja T₁(p_i) és T₁(p_j) egyeneseknek, függőleges távolsága T₁(p_k)-tól nulla. A második lemma alapján a p_k pont függőleges távolsága l_i,j -től nulla. Következésképpen p_i, p_j és p_k kollineárisak és a legkisebb területű háromszög területe nulla. Ha találunk tehát három ilyen egyenest azonnal megállunk és visszatérítjük a (p_i,p_j,p_k) hármast, amely nulla területű háromszöget alkot.

Az algoritmus bonyolultsága:

1. Lépés: O(n)

2. Lépés: O(n²) és létrehoz

metszési csúcsot T₁(S)-ben

3. Lépés: O(n²log n) a második lépésben szerkesztett metszési csúcsok rendezése

4. Lépés: O(n log n).

5. Lépés: Minden v_r csúcsra O(log n) idő alatt találja meg a v_r csúcs pozícióját az A 2-3 fában, frissíti az A 2-3 fát és számítja ki a két háromszög területét. Tehát a szükséges idő: O(m log n) = O(n² log n).

6. Lépés: Mivel minden v_r csúcspontnak két háromszöget szerkesztünk, a szerkesztett háromszögek számának határa O(m) = O(n²). Következésképpen ez a lépés O(n²) időt vesz igénybe.

A fenti algoritmus bonyolultsága tehát: O(n² log n)

Mivel minden egyenes a T₁(S) síkgráfjában megfelel egy pontnak S-ből, az A 2-3 fa pontosan n levelű. Viszont a v_r csúcsok tárolására Ω(n²) tárterület szükséges, tehát az algoritmus ennyi helyet igényel.

Hogyan lehet redukálni az algoritmus által igényelt helyet? A fentiek alapján az algoritmusnak szükséges Ω(n²) tárterület az m darab metszési csomópont tárolására. Valójában nem szükséges az egész eltárolt lista. Ami tényleg érdekel, hogy minden lépésben melyik csúcspont következik az aktuális után. Ez a következő a jelenlegi v_r jobboldalán lévő és a v_r-en áthaladó függőleges egyeneshez a legközelebbi kell legyen. Figyeljük meg, hogy egy ilyen csúcspont a metszéspontja kell legyen két egyenesnek T₁(S)-beli egymásutáni levélnek az A 2-3 fában. Ezért ha tárolunk egy B listát az egymásutáni leveleiről az A 2-3 fának, amik a jelenlegi v_r csúcspont jobboldalán vannak (legtöbb n-1 ilyen van), akkor a B listában a legközelebb lévő, a jelenlegi v_r csúcsponton áthaladó, függőleges egyeneshez, kell legyen a következő csúcspont a fenti algoritmus 5. lépésében.

Ezért, az egész lista létrehozása helyett, egy B 2-3 fát használunk, amelyben az egymásutáni egyenesek metszési csúcsait tároljuk, amelyek jobbra vannak v_r-től. B-nek n-nél kevesebb levele van. Ha a jelenlegi csúcspont v_r, akkor a következő csúcspont megtalálásához megkeressük azt a v_r+1 csúcsot B-ből, aminek legkisebb az x koordinátája. Ekkor v_r-t töröljük B-ből. Miután bejártuk v_r-t, csak négy szomszédos egyenessel váltózhat a viszonya. Feltételezzük, hogy v_r a T₁(p_i) és T₁(p_j) egyeneseknek metszéspontja, a v_r csomópont fölött és a rögtön alatta lévő két egyenes T₁(p_k) illetve T₁(p_h) és, hogy mielőtt bejártuk a v_r csúcspontot a T₁(p_i) a T₁(p_j) fölött volt. Miután bejártuk a v_r-t T₁(p_j) a T₁(p_i) fölött lesz. Ezért mielőtt bejártuk v_r-t az egyenesek sorrendje:

T₁(p_k) T₁(p_i) T₁(p_j) T₁(p_h)

az A 2-3 fában, bejárás után az új sorrend:

T₁(p_k) T₁(p_i) T₁(p_j) T₁(p_h)

Ennek megfelelően a 2-3 B fa frissíthető azáltal, hogy töröljük a metszési csúcspontját T₁(p_k) és T₁(p_i)-nek és T₁(p_j) és T₁(p_h)-nak és beszúrjuk a metszéspontját T₁(p_k) és T₁(p_j)-nek és T₁(p_i) és T₁(p_h)-nak ha a v_r jobboldalán vannak. Mivel a 2-3 B fának n-nél kevesebb levele van, a fenti műveletek O(log n) idő alatt végezhetőek el. Így az 5. lépésben egy csúcs bejárása O(log n) és a tárterület O(n).

Végkövetkeztetések:

Ha a legkisebb háromszög területe nulla, akkor a három csúcspontja kollineáris. Tehát a fenti algoritmus használható arra is, hogy megállapítsuk, létezik-e három kollineáris pont egy ponthalmazon belül. A fenti algoritmus nem a leghatékonyabb. Az eddig ismert leghatékonyabb algoritmus, Edelsbrunner, O'Rourke és Seidel algoritmusa, mely O(n²) idő- és O(n) tárbonyolultságú. Az ismert alsó határ Omega(n log n). A három kollineáris pont létezésére vonatkozó feladat ismert alsó határai szintén O(n²), illetve Omega(n log n). A felső, vagy alsó határok javítása még egy nyílt kérdés a komputacionális geometria tudományán belül.