Delaunay-féle háromszögesítés

(Delaunay Triangulation)

Az eddigi fejezetek során, amikor térképről beszéltünk mindig feltételeztük, hogy nincs domborzat, vagyis minden pont ugyanazon a tengerszint feletti magasságon van. Ez viszont nem mindig igaz. Szükségünk van háromdimenziós térképekre, vagy legalábbis a magasságok váltakozásának feltüntetésére kétdimenziós térkép esetén. Ha például egy A területet szeretnénk valósághűen ábrázolni, akkor kellene ismernünk az A minden p pontjában a p pont magasságát. Természetesen ez lehetetlen, csak bizonyos véges számú példapontnak ismerhetjük a magasságát. Ezekből a magasságokból kiindulva kellene valahogyan megközelíteni, interpolálni a területet.

Legyen azon pontok halmaza, amelyeknek ismerjök a magasságát. Először meghatározzuk a P halmaz háromszögesítését: egy olyan síkfelosztást, amelynek csúcsai a P pontjai és a lapjai háromszögek (kivéve a végtelen lapot). Ezután minden pontot feltolunk a megfelelő magasságba, megfeleltetve ezáltal a háromszögesítés minden háromszögének egy háromdimenziós háromszöget. Az így kapott felületet (poliéderszerű terület) tekinthetjük az eredeti terület egy megközelítésének.

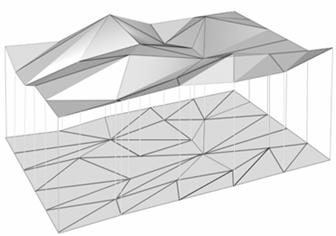
Példapontok alapján szerkesztett poliéderes terület

Feltevődik a kérdés, hogy a P ponthalmazt hogyan háromszögesítsük, mert általában ez többféleképpen történhet. Melyik háromszögesítés fogja a legvalósághűbb ábrázolást adni?

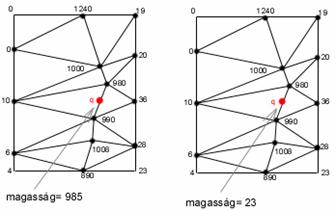
Egy élet felcserélve nagy különbségek lesznek

A b) ábrán a gond az, hogy a q pont magasságát két eléggé távoli pont határozza meg, vagyis a q pont két “lapos” háromszög hosszabbik oldalának van a közepén. A háromszögek “lapossága” okozza a gondot. Tehát úgy tűnik, hogy az a háromszögesítés, amelyben kicsi szögek vannak, nem jó. Tehát rangsoroljuk a háromszögesítéseket a legkisebb szögeiket összehasonlítva. Ha két háromszögesítésben a legkisebb szögek mértéke megegyezik, akkor tekintjük a második legkisebb szöget, és így tovább. Mivel egy adott P véges ponthalmaznak csak véges számú háromszögesítése létezik, kell legyen egy optimális háromszögesítés, amelyiknél a legkisebb szög nagyobb az összes többi háromszögesítés legkisebb szögénél. Ez lesz a keresett háromszögesítés.

1. Síkbeli pontok háromszögesítése

Legyen egy síkbeli pontokat tartalmazó ponthalmaz.

Értelmezés: A P háromszögesítése egy S maximális síkfelosztás, amelynek csúcsai P-ből vannak, vagyis egy olyan S síkfelosztás, amelynek csúcsai P-ből vannak és bármely olyan él, amely nem eleme S-nek, metsz legalább egy élet S-ből.

Észrevehetjük, hogy a háromszögesítés után kapott háromszögeket egyesítve megkapjuk a konv(P) konvex burkolót. Egy háromszögesítés háromszögeinek és éleinek száma ugyanannyi bármilyen háromszögesítés esetén. A pontos számuk függ attól, hogy a P pontjai közül hány található a P konvex burkolójának határán (ezek a pontok lehetnek a konvex burok határának élein is, nem feltétlenül kell mind csúcsai legyenek a konvex buroknak).

5.1. Tétel: Legyen P n síkbeli pontot tartalmazó halmaz. Feltételezzük, hogy a pontok nem mind kollineárisak és jelöljük k-val a P azon pontjainak szánát, amelyek a konv(P) határán vannak. Ekkor a P bármely háromszögesítésében 2n-2-k háromszög és 3n-3-k él van.

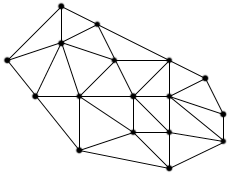
n=16, h=9

: 2 x 16 - 2 - 9 = 21

élek: 3 x 16 - 3 -9 = 36

Bizonyítás: Legyen T_p a P háromszögesítése és m a T_p háromszögeinek száma. Ekkor a háromszögesítés lapjainak száma n_l = m+1. Minden háromszögnek van három oldaléle és a végtelen lapnak pedig k. Minden él két lapot határol, tehát a T_p éleinek száma n_é = . Felhasználjuk az Euler-féle képletet:

n_cs – n_é + n_l = 2.

Behelyettesítve a megfelelő értékeket kapjuk, hogy

n – + m + 1 = 2

2n – 3m – k + 2m + 2 – n = 0

2n – 2 – k – m = 0

m = 2n – 2 – k

Legyen T_p a P egy háromszögesítése és tételezzük fel, hogy m háromszöget tartalmaz. Tekintjük a T_p háromszögeinek 3m darab szögét növekvő sorrendbe rendezve:

,

A(T_p) = a T_p szögvektora(angle-vector of T_p).

Legyen egy másik háromszögesítése P-nek és a megfelelő szögvektor. Azt mondjuk, hogy A(T_p ) >, ha úgy, hogy

.

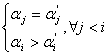Egy T_p háromszögesítést szög-optimálisnak nevezünk, ha a P bármely háromszögesítése esetén. Amint a fejezet elején láttuk, minket a szög-optimális háromszögesítések érdekelnek.

A továbbiakban tanulmányozzuk, hogy egy háromszögesítés mikor szög-optimális.

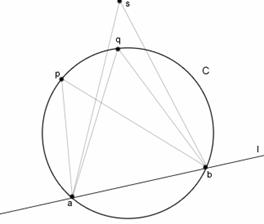
5.2. Tétel (Thálesz tétele): Legyen C egy kör és l egyenes, amely metszi a kört az a és b pontokban. Legyenek a p,q,r,s pontok az l egyenes ugyanazon oldalán úgy, hogy , . Ekkor .

Értelmezés: Legyen a T_p háromszögesítés egy éle. Ha e nem a végtelen lap éle, akkor két háromszög, például és háromszögek közös éle. Ha a egy konvex négyszög, akkor egy új háromszögesítést kapunk lecserélve a élet a élre. Ezt a műveletet nevezzük élcserének (edge flip).

A T és háromszögesítések szögvektoraiban a különbség annyi lesz, hogy az szögeket helyettesíteni kell az szögekkel (lásd V.5. ábra).

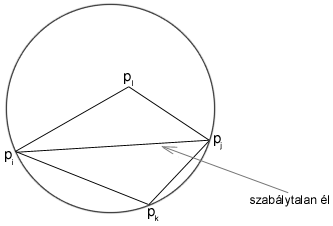
Értelmezés: Azt mondjuk, hogy az él szabálytalan (illegal edge), ha .

Tehát egy él akkor szabálytalan, ha tudjuk (lokálisan) növelni a minimális szöget egy él felcserélésével. (Egy olyan élet, amelyik a konvex burkoló határán van, nem szabálytalan, vagy szabályos lokális Delaunay-élnek nevezünk).

Megjegyzés: Legyen T egy háromszögesítés, amelyben e szabálytalan él és az e lecserélésével kapott háromszögesítés. Ekkor .

Az alábbi tétel egy jellemzését adja a szabálytalan éleknek anélkül, hogy szögeket számolna.

5.3. Tétel: Tételezzük fel, hogy a él a és háromszögek közös éle és legyen C a háromszög köré írt kör. A él akkor és csak akkor szabálytalan, ha a . Ezen kívül, ha a négyszög konvex és nem körbeírható, akkor a és élek közül csak az egyik szabálytalan.

Értelmezés: Azt mondjuk, hogy egy háromszögesítés szabályos, ha nem tartalmaz szabálytalan éleket.

Megjegyzés: Belátható, hogy egy szöoptimális háromszögesítés szabályos.

Egy tetszőleges háromszögesítésből egyszerűen eljuthatunk szabályos háromszögesítéshez: a szabálytalan éleket cserélgetjük addig, amíg minden él szabályos lesz.

Algoritmus SzabályosHáromszögesítés(T)

Bemenet: A P egy tetszőleges T háromszögesítése

Kimenet: A P egy szabályos T háromszögesítése

BEGIN

AMÍG T tartalmaz egy szabálytalan élet VÉGEZD EL

Legyen és a élhez tartozó háromszögek

Cseréld fel a élt a éllel

(AMÍG) vége

END.

Megjegyzés: Az algoritmus megáll, mert a szögvektor nő minden cikluslépés után. Mivel csak véges számú háromszögesítése létezik P-nek, egy idő után a végére jutunk. Ekkor az eredmény egy szabályos háromszögesítés. Mindezek ellenére az algoritmusnak csak elméleti jelentősége van, mert túl lassú.

Delaunay-háromszögesítés

Az előző paragrafusban láttuk, hogy egy véges P ponthalmaz esetén vannak módszerek a P szabályos háromszögesítésére. Bevezetünk most egy speciális háromszögesítés-típust, az ún. Delaunay-féle háromszögesítést és be fogjuk látni, hogy egy háromszögesítés akkor és csakis akkor szabályos, ha Delaunay-féle háromszögesítés. A Delaunay-féle háromszögesítés előnye, hogy nagyon pontos és világos geometriai szerkezete van.

Egy adott ponthalmaz esetén Delaunay-gráfnak nevezzük (jelölés: GD(P)) a Vor(P) Voronoi-diagram duál gráfját. Vagyis a GD(P) csúcsai a P-beli pontok és két csúcs közt akkor és csakis akkor van él, ha a csúcsoknak megfelelő Voronoi-celláknak van közös élük.

(A Delaunay-gráfot az orosz Borisz Nikolajevics Delone matematikusról nevezték le. Mivel a műveit franciául írta, a neve is a francia helyesírás szerint maradt fenn).

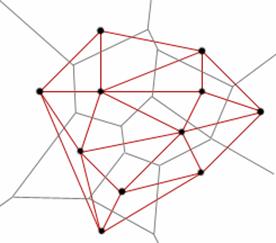
A P ponthalmaz Voronoi diagramja és Delaunay gráfja

A továbbiakban felelevenítjük a Voronoi-diagramok két fontos tulajdonságát, amelyek segítségével könnyen jellemezhetjük a Delaunay-gráfot.

4. Tétel:

(i) Egy q pont akkor és csakis akkor Voronoicsúcs, ha a legnagyobb kör tartalmaz legalább 3 P-beli pontot határán.

(ii) A és pontok felezője akkor és csakis akkor határoz meg egy élet a Vor(P)-ben ha ú.h. tartalmazza a és pontokat a határán, de nem tartalmaz egyetlen más P-beli pontot sem.

5. Tétel: Egy síkbeli ponthalmaz Delaunay-gráfja síkgráf.

Biz: Mindenekelőtt vegyük észre, hogy a 4.Tétel(ii) alpontját a köv. képpen írhatjuk át:

(ii)’ A szakasz akkor és csakis akkor él a Dg(P) Delaunay gráfban, ha létezik egy zárt körlap, amely tartalmazza a határán a és pontokat és nem tartalmaz más P-beli pontot.

Legyen a , valamint a kör középpontja által meghat. háromszög. Legyen egy másik él Dg(P)-ben, és egy zárt körlap ill. egy háromszög ugyanúgy megszerkesztve mint az előbb.

Mivel és üresek nem tartalmazza háromszög egyetlen csúcsát sem és fordítva. Tehát ha akkor a háromszögnek az egyik éle, amelyik a középpontjából indul ki kell messe a egyik, a középpontjából kiinduló élet. De ez lehetetlen, mert ezek a szakaszok (különböző) diszjunkt Voronoi cellákból vannak. Tehát a és háromszögek – így a és szakaszok sem – metszhetik egymást.

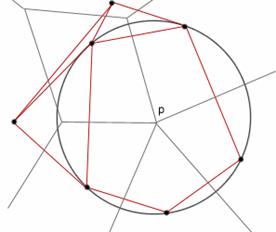
A Dg(P) tartalmaz egy-egy csúcsot minden Voronoicellának megfelelően és egy-egy élet minden Voronoi-él esetén. Tehát létezik egy bijektív megfeleltetés a Dg(P) korlátos lapjai és a Voronoi-csúcsok között. Azok az élek, amelyek ugyanazt a lapot határolják a Dg(P)-ben, megfelelnek a laphoz rendelt Voronoi csúcsból kiinduló Voronoi éleknek (lásd V.7. ábra). Ha egy P Voronoi csúcs foka k, akkor a hozzárendelt lap ( Dg(P)) csúcsai amelyek Voronoi cellái érintkeznek a P-ben. Ha egy halmaz pontjai általános helyzetben vannak, vagyis 4 pont nincs egy körön, akkor minden Voronoi-csúcs foka három, tehát a Delaunay gráf lapjai háromszögek. Innen szarmazik a Delaunay-háromszögesítés elnevezés (a Delaunay-gráf helyett).

Általában egy halmaz Delaunay háromszögesítése a halmaz Delaunay-gráfjának a háromszögesítését jelenti olyan értelemben, hogy háromszögesítjük azokat a lapokat, amelyek még nem háromszögek. Ha a pontok ált. helyzetüek, akkor a halmaznak egyetlen Delaunay háromszögesítés létezik, általában viszont több is van, amelyek a szabalyosság szempontjából mind ekvivalensek függetleneül a lapok háromszögesítésétől.

A 4. Tételt átfogalmazhatjuk a Delaunay-gráf fogalmáthasználva a köv. képpen:

6. Tétel: Legyen , P véges ponthalmaz. Akkor

(i) , , P akkor és csakis akkor a Dg(P) ugyanazon lapjának csúcsai, ha a köré írt kör nem tartalmaz a belsejében más P-beli pontokat.

(ii) , meghat. egy étet a Dg(P)-ban egy zárt körlap, amelyre a , és nem tartalmaz más pontot P-ből.

Következmény: Legyen egy véges ponthalmaz és T a P egy háromszögesítése. Ez a háromszögesítés akkor és csakis akkor Delaunay- háromszögesítés, ha a háromszögesítés bármely háromszöge köré írt kör nem tartalmaz a belsejében P-beli pontokat.

7. Tétel: Legyen egy véges ponthalmaz. A P egy T háromszögesítése akkor és csakis akkor szabályos, ha Delaunay- háromszögesítés.

T szabályos háromszögesítés T Delaunay- háromszögesítés

Bizonyítás:

„” azonnali az értelmezések következtében és a 3. tétel alapján

„” red. ad. abs.

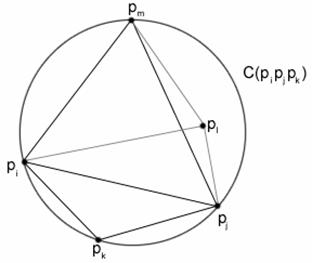Tételezzük fel, hogy T szabályos háromszögesítés, de nem Delaunay- háromszögesítés. A 6. tétel alapján ez azt jelenti, hogy létezik úgy, hogy a háromszög köré írt C() kör tartalmaz egy pontot a belsejében. Legyen e= a éle, ahol . A T háromszögesítés összes párja közül kiválasztjuk azt a párt, amelyre a maximális. Tekintsük a háromszöget, amelynek az e éle közös a háromszöggel. Mivel T szabályos, következik e is szabályos. Ekkor az 5.3 tétel alapján int C(). A C() kör tartalmazza a belsejében a C() kör azon részét, amely az e-nek ugyanazon oldalán van mint a . Tehát C(). Tételezzük fel, hogy az az oldal, amelyre a és háromszögek nem metszik egymást. Ekkor a > , ami ellentmond a pár megválasztásának.

8. Tétel: Legyen egy véges ponthalmaz. Akkor a P bármely szög-optimális háromszögesítése Delaunay-háromszögesítés. Sőt, bármely Delaunay-háromszögesítés maximalizálja a P összes háromszögesítései közül a legkisebb szöget.

Bizonyítás: Mivel minden szög-optimális háromszögesítés szabályos kell legyen, a 8. tétel alapján következik, hogy P bármely szög-optimális háromszögesítése Delaunay-háromszögesítés

Amikor P általános helyzetben van, akkor egyetlen szabályos háromszögesítés van, amely tehát egyetlen szög-optimális háromszögesítés, nevezetesen az egyetlen Delaunay-háromszögesítés, amely egybeesik a Delaunay-gráffal.

Amikor P nincs általános helyzetben, akkor a Delaunay-gráf bármely háromszögesítése szabályos, de ezek közül nem mindenik szög-optimális. Mégis a szögvektoraik nem sokban különböznek. Felhasználva Thálesz tételét kimutatható, hogy egy körbeírható négyszög háromszögesítése során kapott háromszögekben a legkisebb szög ugyanannyi, tehát a legkisebb szög független a háromszögesítéstől. Mivel egyik háromszögesítés ezek közül optimális kell legyen, következik, hogy ennek a legkisebb szögnek a mértéke maximális kell legyen a pothalmaz minden háromszögesítése közül.

A Delaunay-háromszögesítés meghatározása

A IV. fejezetben láttuk, hogyan határozhatjuk meg a Voronoi-diagrammot. Ha már meg van szerkesztve a Voronoi-diagramm, akkor ebből kiindulva gyorsan megszerkeszthető a Delaunay-háromszögesítés. Ebben a fejezetben egy másik megközelítést mutatunk be.

Vázlatosan az algoritmusnak a következő struktúrája lesz:

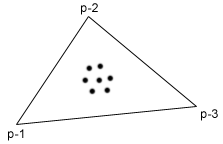
(i) Először hozzáadunk a P halmazhoz még három pontot: úgy, hogy a P halmaz legyen teljesen a háromszög belsejében. Legyen . A P halmaz Delaunay-háromszögesítése helyett a halmaz Delaunay-háromszögesítését fogjuk meghatározni.

(ii) Kiindulva a halmaz egy részhalmazának Delaunay-háromszögesítéséből, hozzáadunk véletlenszerűen egy pontot és megszerkesztjük az új halmaz Delaunay-háromszögesítését. Három teendőnk van:

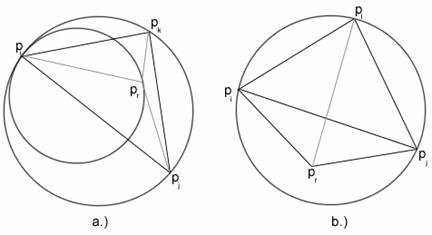
(a) Ha az eddigi pontok háromszögesítése során kapott például háromszög belsejében van, akkor összekötjük a pontot a háromszög ,, csúcsaival. (V.10.a) ábra)

(b) Ha egy e élen található, akkor összekötjük -et annak a két háromszögnek a szemközti csúcsaival, amelyeknek az e közös élük. (V.10.b) ábra)

(c) Az előző lépésekben a háromszögesítéshez hozzáadott új élekkel szabálytalan élek keletkezhetnek. Ezeket kell élcserével szabályos élekké alakítanunk ahhoz, hogy a pont hozzáadásával keletkezett háromszögesítés Delaunay-háromszögesítés legyen.

(iii) A halmaz Delaunay-háromszögesítéséből kitöröljük mindazokat az éleket, amelyek a P pontjait kötik össze az csúcsaival.

Algoritmus Delaunay-háromszögesítés(P)

Bemenet: A sík n pontját tartalmazó P halmaz.

Eredmény: A P Delaunay-háromszögesítése.

BEGIN

1. Legyen három olyan pont, amelyre

2. T = {} {inicializálás}

3. P = {} véletlenszerű sorrend

4. FOR r = 1 to n DO

5. Keress egy háromszöget, amely tartalmazza -t

6. Ha , akkor

7. Szerkessz éleket a és ,, csúcsok közé, felosztva a háromszöget 3 új háromszögre

8. Szabályosítél(, , T )

9. Szabályosítél(, , T )

10. Szabályosítél(, , T )

Különben

11. Szerkessz élet a és , valamint és oldal másik felén lévő háromszög csúcsa közé, felosztva a két érintkező háromszöget négy háromszögre

12. Szabályosítél(, , T )

13. Szabályosítél(, , T )

14. Szabályosítél(, , T )

15. Szabályosítél(, , T )

( FOR) vége

16. Töröld ki a pontokat minden belőlük kiinduló éllel együtt a T-ből

END.

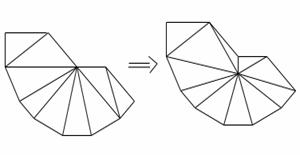
A továbbiakban tárgyaljuk hogyan lehet a 7. vagy 11. sorok után kapott háromszögesítést Delaunay-háromszögesítéssé alakítani. A 8. tétel értelmében egy háromszögesítés Delaunay-háromszögesítés, ha minden él szabályos. A SZABÁLYOSÍTÉL algoritmusban tehát addig kell élcseréket végezni, amíg szabályos éleink lesznek csak. Nézzük milyen élek válhatnak szabálytalanná egy pont beszúrása esetén. Észrevehetjük, hogy egy él, amelyik eddig szabályos volt, csak akkor válhat szabálytalanná, ha valamelyik háromszög, amelyet határol, megváltozik. Tehát az új háromszögek oldalait kell vizsgáljuk a SZABÁLYOSÍTÉL algoritmus során. Ha a SZABÁLYOSÍTÉL algoritmus felcserél egy élet, más élek válhatnak szabálytalanná. Tehát a SZABÁLYOSÍTÉL algoritmus rekurzívan hívja önmagát, amíg talál ilyen szabálytalan éleket.

Algorimus SZABÁLYOSÍTÉL(, , T )

{a pontot szúrjuk be és a T háromszögesítés élét lehet, hogy kell cserélni, mert szabálytalan}

BEGIN

1. Ha szabálytalan, akkor

2. Legyen a szomszédja a mentén

3. Cseréld ki a élet a éllel

4. SZABÁLYOSÍTÉL(, , T )

5. SZABÁLYOSÍTÉL(, , T )

END.

Az algoritmus második sorában lévő tesztelést ( szabályos-e) általában a 3. tétel segítségével vizsgálhatjuk. Esetünken azonban kicsit bonyolultabb a pontok jelenléte miatt. Erre még visszatérünk, előbb azonban lássuk be az algoritmus helyességét.

Az algoritmus helyessége érdekében be kell lássuk, hogy a SZABÁLYOSÍTÉL algoritmusok hívása után egyetlen szabálytalan él sem marad, amelyet ne vizsgáltunk volna. Egy pont beszúrása után keletkezett bármely új él a pontból indul ki. Az alapvető észrevétel (alább bizonyítjuk) az, hogy bármely új él szabályos él lesz, tehát nem szükséges tesztelni azt. A Delaunay-háromszögesít eljárásban pedig csak az új élekre nem hívtuk meg a a SZABÁLYOSÍTÉL algoritmust, a többi összes lehetséges szabálytalan élre meghívtuk. Tehát az algoritmus helyes.

A SZABÁLYOSÍTÉL algoritmus nem lesz végtelen ciklus, mert minden élcsere növeli a háromszögesítés szögvektorát.

9. Tétel: A Delaunay-háromszögesít és SZABÁLYOSÍTÉL algoritmusok során egy új pont beszúrásával keletkezett bámely új él az {} halmaz Delaunay-gráfjának éle.

Bizonyítás: Tekintjük először a , , (és esetleg ) éleket, amelyeket a (esetleg ) háromszög felosztása után kaptunk. Mivel egy háromszög a Delaunay-háromszögesítésben a pont hozzáadása előtt, a háromszög köré írt C kör nem tartalmaz a belsejében egyetlen pontot sem, ahol s<r.

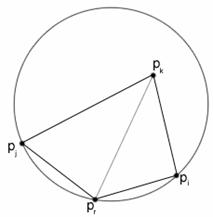
Összenyomva a C kört, találunk egy olyan C’ kört (V.13.a) ábra), amely átmegy a és pontokon és benne van a C-ben. Mivel , következik, hogy C’ nem tartalmaz a belsejében egyetlen pontot sem, ahol s<r. Tehát egy Delaunay-él a pont hozzáadása után a 6. tétel (ii) alapján. Hasonlóan , (és esetleg ) esetén.

Tekintsünk a továbbiakban egy élet, amelyet a SZABÁLYOSÍTÉL algoritmus változtatott meg. Ilyen esetben egy élét cseréljük a -ből kiinduló élre. Mivel a pont hozzáadása előtt a Delaunay-háromszög volt, következik, hogy (különben a él nem lenne szabálytalan), tehát össze tudjuk nyomni a C kört egy C’ körre, amelyik tartalmazza a határán a és pontokat és a belsejében egyetlen más pontot sem. Tehát a él szabályos.

Még két feladatunk maradt:

a) megtalálni azt a háromszöget, amely tartalmazza apontot a Delaunay-háromszögesít algoritmus 5. sorában

b) a SZABÁLYOSÍTÉL algoritmus 2. sorában a szabályosságot vizsgáló tesztelést helyesen elvégezni a pontokkal.

Az a) feladat megoldása érdekében a következőképpen járunk el: miközben szerkesztjük a Delaunay-háromszögesítést, felépítünk egy D irányított, nem ciklikus gráfot, a pontok lokalizálása érdekében. A D levelei az aktuális háromszögesítés háromszögeire mutatnak. A gráf közbeeső csomópontjai (amelyek nem levelek) háromszögek voltak valamely előző háromszögesítés során, de felbontottuk őket.

Kezdetben a D gráf egyetlen csomópontból áll, háromszögnek megfelelően. Tételezzük fel, hogy egy adott pillanatban az aktuális háromszögesítés háromszögét felbontjuk 3 vagy 2 háromszögre. Ez azt jelenti, hogy hozzáadunk a D-hez 3 vagy 2 új levelet és a háromszögnek megfelelő levél átalakul közbeeső csomóponttá, amely a 3 vagy 2 új levélre mutat. Hasonlóan, amikor helyettesítjük a és háromszöget a és háromszögekkel egy élcsere során, létrehozunk új leveleket az új háromszögeknek és kitesszük a megfelelő mutatókat.

Nézzük hogyan lokalizáljuk apontot, ha rendelkezésünkre áll a pont hozzáadása előtti háromszögesítéshez rendelt D gráf. Kezdjük a D gyökerével, amely megfelel a háromszögnek. Megvizsgáljuk a gyökér alatti csomópontokat, hogy eldöntsük melyik háromszögben van és az illető csomópontba lejövünk. Ezt folytatjuk, amíg eljutunk a D egy leveléhez. Ez a levél felel meg az aktuális háromszögesítés azon háromszögének, amelyik tartalmazza a pontot. (Mivel minden csomópont foka legfennebb három, a keresés lineáris időt igényel a keresési út csomópontjainak (a -t tartalmazó háromszögek) számában).

Példa:

a.) kezdeti háromszögesítés

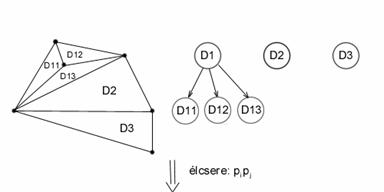b.) a pr beszùrása

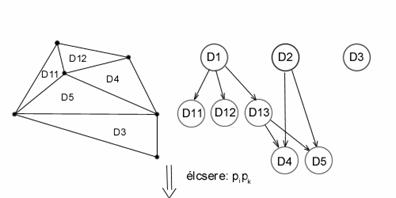
c.) elsô szabályosítás

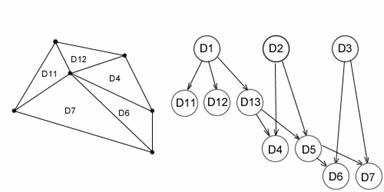
d.) második szabályosítás

Egy pr pont beszùrása esetén a Delaunay -esítés és a Delaunay gráf változása

A b) feladat megoldása érdekében a következőképpen választjuk meg a pontokat : (3M,0), (0,3M), (-3M,-3M), ahol M a P pontjainak moduluszban vett koordinátái közül a legnagyobb. Tehát P. (Elméletileg minnél nagyobb koordinátákat kellene választani de ezek csak bonyolítanák a számításokat)

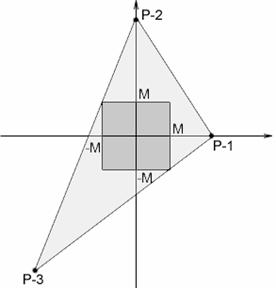
A szabályosság vizsgálata esetén mégsem használjuk ezeket a koordinátákat. Ehelyett, növelve esetleg AZ M értékét, feltételezzük, hogy bármely 3P-beli pont által meghatározott körön kívül található, bármely 3P{}-beli pont által meghatározott körön kívül található, bármely P{,}-beli pont által meghatározott körön kívül található.

Így a szabályosságot a köv. Képpen vizsgáljuk :

-legyen a vizsgált él .

1.eset : i,j<0

Ebben az esetben úgy döntjük el, hogy szabályos él, mivel a oldalait nem rontjuk el.

A többi eset során legyen és a él két oldalán levő - ek harmadik csúcsai.

2.eset: i,j,k,l>0

Ez a normális eset. A él szabálytalan int().

3.eset: egyik i,j,k,l közül negatív.

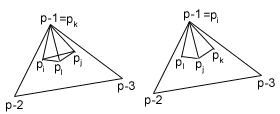
Nem akarjuk, hogy egy speciális pont elrontson a P pontjai közti Delaunay éleket! Ezért, ha i<0 vagy j<0 úgy döntjük el, hogy szabálytalan, tehát helyettesítjük -val, különben szabályos.

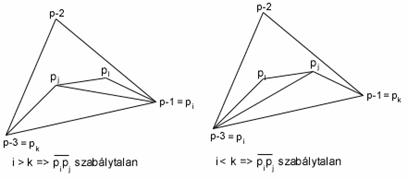
4.eset: két negatív van Az i,j,k,l indexek közt. Ha i,j<0 vagy k,l<0 akkor az első esetben vagyunk.

Tételezzük fel, hogy az egyik az {i,j} és egyik a {k,l} közül negatív. Ha az i,j közül a negatív index < k,l közül a negatív szabályos, különben szabálytalan.

5.eset: Három index negatív. Ez az eset nem állhat fenn, mert ha i,j<0 1. eset, és ha k,l<0 szintén nem lehet mert az egyik a pontok közül az éppen beszúrt pont, tehát nem lehet <0 indexü.

A Delaunay háromszögesítés alg. során szerkesztett háromszögesítés háromszögeinek száma legfennebb 9n+1.