A VORONOI DIAGRAM dokumentációja

1. Bevezető helyett
2. Delaunay háromszög
3. Voronoi diagram
4. A Delaunay háromszög és a Voronoi diagram közti kapcsolat
5. Történelmi áttekintés
6. A Fortune algoritmus elméleti leírása
"pont esemény"
"kör esemény"
7. A tulajdonképpeni algoritmus
8. Adatstrukturák a Fortune algoritmusban
9. A Voronoi diagram adastrukturája
10.A parabolikus görbe adatstruktúrája
11.Az események tárolására szolgáló adastruktúra

1.Bevezető helyett

Dolgozatunkban első részében rövid elméleti bemutató található a Voronoi diagramról , a Delaunay háromszögről és ezek kapcsolatáról. Majd pár sorban a történelmi áttekintés következik. Ezután az általunk használt Fortune algoritmus általános leírása található,
majd az ehhez szükséges adatstruktúrák. Legvégül a Java Appletek konkrét dokumentációja.

2. Delaunay háromszög

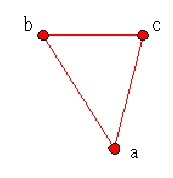
Legyen egy ponthalmaz a síkban. Természetesen sokféleképpen megszerkeszthető a pontok által alkotott háromszögháló, de ahhoz , hogy a Delaunay kritériumnak is megfeleljen a pontokat úgy kell összekötnünk , hogy az így kialakult háromszögháló
maximalizálja a minimumát a háromszögek belső szögeinek.

1.1.ábra Ponthalmaz a síkban

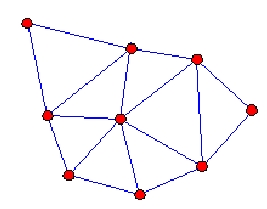
1.2.ábra Delaunay háromszögek

A Delauney háromszög egyik alapvető jellemzője, hogy a háromszög köré írt kör nem tartalmaz más ponthalmazbeli pontot. mint saját csúcsai.

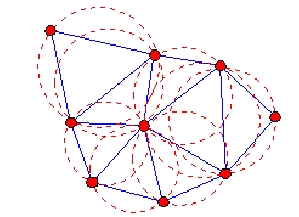
1.3.ábra Delaunay háromszögek tulajdonsága

3. Voronoi diagram

Egy síkbeli ponthalmaz Voronoi diagramja a sík poligonális területekre való felosztása,
ahol minden egyes régió olyan pontok halmaza a síkban, amely valamely bemeneti ponthoz közelebb van, mint bármely másik bemeneti ponthoz.

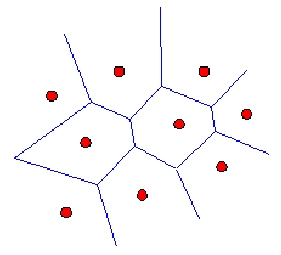
2.1.ábra Voronoi diagram

4. A Delaunay háromszög és a Voronoi diagram közti kapcsolat

A Voronoi diagram valójában a Delauney háromszögelés geometriai duálisa, azaz egyikből a másik megkapható. A módszer az, hogy a Delaunay éleinek középpontján
átmenő merőleges vonalakat behúzzuk.

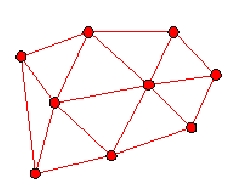
3.1 .ábra Delaunay és Voronoi közti kapcsolat

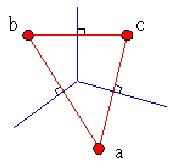
3.2. ábra Delaunay háromszög Voronoi diagrammá alakítása

5. Történelmi áttekintés

A Vorinoi diagram az algoritmikus geometria egyik klasszikus problémája. Az eredete 1850- re nyúlik vissza és Dirichlettől származik. A konkrét matematikai leírást azonban Voronoi fogalmazta meg 1908 - ban.
Az első komolyabb próbálkozás az algoritmus leírására Green és Sibson nevéhez fűződik, bár a Voronoi diagram már rég ismert volt. Ennek az algoritmusnak a bonyolultsági foka még O(n2) volt, de 1975-ben Shamos és Hoey bemutatja az első
O(n log2 n) bonyolultságú algoritmust ami a divide et impera módszert használta.
1985-ben Fortune bemutatott egy elegáns megoldást a Voronoi diagram meghatározására.
Edelsbruner és Seidel 1986- ban felfedezték a kapcsolatot a Voronoi diagram és a konvex burkoló között, közösen kidolgoztak egy új módszert az algoritmus leírására.

Napjainkban Voronoi diagram sok gyakorlati alkalmazása ismert. Számos geometriai
problémát lineáris időben megoldhatunk segítségével, mint például a legközelebbi szomszéd problémája, minimális feszítőfa keresése, Delaunay triangularizáció és a legnagyobb kör keresése.

6. A Fortune algoritmus elméleti leírása

Fortune algoritmusában egy a számítógépes grafikában és az algoritmikus geometriában gyakran használt módszert alkalmazott, ú.n. seprő egyenest. Az algoritmus alapötlete nagyon egyszerű, időbonyolultsága legrosszabb esetben O(n log2 n) ahol n a bemeneti pontok száma.
A módszer Fortune 3D-s térbeni megfigyelésein alapul. Ö minden egyes P-beli pontot
egy fordított kúp csúcsának tekintett, amint az alábbi ábra szemlélteti. Mozgatunk egy PI síkot, amely metszi a kúpokat és az xy síkot. A PI sík az xy síkkal 45?-os szöget zár be, ugyanúgy mint a kúp alkotója.

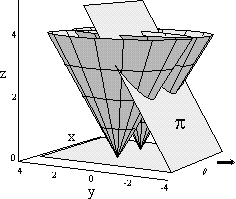
A Fortune algoritmusban minket a PI sík és a kúpok metszete érdekel. Ezen metszetek parabolaívek által meghatározott PI görbét írnak le. A parabolaívek akkor találkoznak amikor két szomszédos kúp metszi egymást. A két kúp xy síkra való vetülete az a félegyenes, amelyen a Voronoi él lesz.
Tekintsük a seprő sík és a kúpok vetületét az xy síkra, ekkor a seprő egyenest és a FI görbe vetületét kapjuk. A következő ábra szemlélteti ennek a görbének a fontosságát.
Tulajdonképpen a Voronoi diagram a görbe mögött jön létre, míg a görbe előtt nem
tudunk semmit róla.

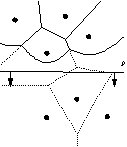
Az ábrából látható, hogy a parabolikus görbe topológiai szerkezete a seprő egyenes xy síkon való mozgásával változik. Felvetődik egy fontos kérdés : mikor és hogyan változik
a görbe topológiai struktúrája. Definiáljunk két fogalmat : "pont esemény" és "kör esemény" . Ezek segítségével válaszolhatunk a fenti kérdésre.

"pont esemény"

"?Pont esemény" az amikor a görbén egy új parabola ív jelenik meg. Ez akkor következik be amikor a seprő egyenes egy P-beli pi pontot talál. Ekkor a PI sík először érinti a pi által
meghatározott kúpot, mivel a kúpnak és a síknak megegyezik a dőlésszöge, a kettejük metszete egyenesként jelenik meg a kúp felületén. Ezt az egyenest ha levetítjük az xy síkra akkor egy 0-ra redukált parabolát kapunk. Ez a parabola a PI sík előrehaladtával fokozatosan kinyílik. Amikor egy új ív jön létre, két részre osztja a létező ívet és a görbe részévé válik.

"kör esemény"

Ez akkor valósul meg, amikor egy parabolaív egy ponttá húzódik össze és eltűnik a görbéből. Legyen ßj egy ilyen ív és ßi illetve ßk két szomszédos íve mielőtt a ßj eltűnne.
Ezen ívek pk, pi és pj pontok által meghatározottak. Amikor ßj eltűnik, mindhárom ív egy
közös q ponton halad keresztül. A q és a seprő egyenes közötti távolság ekkor megegyezik a q és a pk, pi , pj közti távolsággal. Ez a három pont egy q középpontú kört határoz meg . A q pont egy Voronoi csúcs lesz.

7. A tulajdonképpeni algoritmus

A fentiekben ismertettük a Fortune módszer alapvető elemeit, most írjunk egy pár szót a befejezési feltételről. Mikor az összes pont a seprő egyenes mögött van és minden eseményt lekezeltünk, még nincs vége Voronoi diagram kirajzolásának. Meg kell rajzolnunk a félegyeneseket is. Mivel ez a számítógép képernyőjén nem megvalósítható, a diagramot egy téglalappal vettük körül amely széleinél a félegyenesek véget érnek.

A következő algoritmus a Fortune módszer magja.

VORONOI_DIAGRAM(P)
Bemenet : egy síkbeli P ponthalmaz
Kimenet : A Voronoi diagram : Vor(P)
{
A Q eseményfa inicializálása az összes pont eseménnyel
Amíg Q nem üres végezd
{
vedd ki a legnagyobb y koordinátájú eseményt Q-ból
Ha az esemény pont esemény (pi-re)
akkor HANDLE_POINT_EVENT(pi)
másként HANDLE_CIRCLE_EVENT(pi)
vedd ki az eseményt Q-ból
}
a Voronoi diagram kirajzolása
}

8. Adatstrukturák a Fortune algoritmusban

A Fortune módszer a legnépszerűbb megoldás a Voronoi diagram megépítésére .
Három adastruktúrára van szükségünk : egy amelyben a Vornoi diagramot tároljuk,
kettő peddig a seprő folyamat implementációjához (pont és kör események, illetve a parabolikus görbe).

9. A Voronoi diagram adastrukturája

Ez az adastruktura három másiknak a kombinációja. A Voronoi diagram Voronoi cellákból, Vornoi élekből és csúcsokbül áll. Mindháromnak külön adatstrukturája van, természetesen egymással kapcsolatban állnak az alábbi ábra szerint.

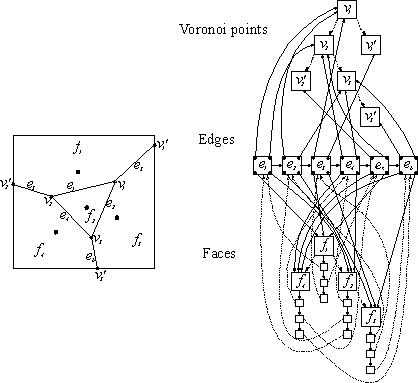
ábra A Voronoi diagram adastrukturája

Készítsük el a Voronoi diagramot miután az összes pontot feldolgoztuk. A félegyenesek és a diagramot határoló téglalap metszetét számoljuk ki. Ezeket a pontokat Voronoi pontoknak vehetjük. Ez a parabolikus görbe fájának azon levei segítségével lehetséges , amelyek a fában maradnak az összes pont feldolgozása után.Ezek a levelek fogják alkotni azokat a Voronoi éleket, amelyek nincsenek teljesen definiálva a feldolgozás után.

10. A parabolikus görbe adatstruktúrája

A parabolikus görbe tárolására a bináris fa a legcélszerűbb.Ez nem csak a gyors kezelhetőség, hanem a görbe topologikus struktúrájából következően is a legoptimálisabb megoldás.

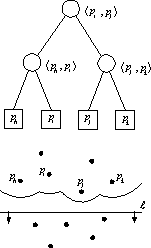
A parabolikus görbe topológiai struktúrájának ábrázolása.

A p. görbe íveit a bináris fa levelei ábrázolják, míg két ív találkozását a közbelső csúcsok alkotják.A bal oldali parabolaívet a bal oldali levél ábrázolja, balról a második a fában balról a következő parabolaív és így tovább.

A legkényesebb kérdés a bináris fából történő törlés illetve új részek hozzáadása.Láttuk, hogy pont esemény esetén új ív jelenik meg a görbében kettéosztva az illető pontól kezdve a régi ívet. Az adatstruktúrában ez úgy jelenik meg, hogy a kettéosztott ívnek megfelelő levelet részfával helyettesítjük. Az alábbi ábrán a részfának három csúcsa van,
a középső felel meg az új ívnek, a másik kettő peddig a régi ív kettéválasztott részeinek.

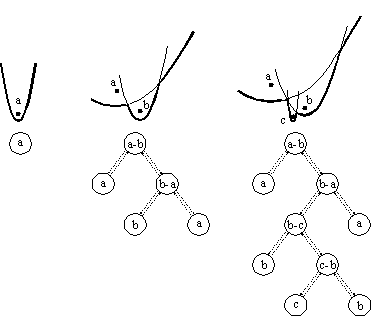
Amint említettük kör esemény esetén az ív leredukálodik egy pontra és eltünik a görbéből.Ekkor a binárisfából a megfelelő levelet törülnünk kell, viszont ezzel együtt a szülőcsúcsot is és a második köztes csúcs a két szomszédos ív tallálkozási pontját fogja jelenteni. A kör eseménye határozza, melyik ívet kell törölni. Mindkét szomszédja az éppen eltünő csúcs jobb és bal leveleként van ábrázolva a fában.Az első csúcsot könnyen megkaphatjuk, mivel ez az eltünő csúcs szülője.A második már körülményesebb, meg kell határoznunk, hogy az eltűnő ív által meghatározott pont melyik oldalán van a második csúcs. Ez úgy van meghatározva mint két keresési irány kereszmetszete.
Az első az eltünő ívtől kezdődik, a második a baloldali (ha balról választjuk el az ívet ) vagy a jobboldali (ha jobbról választjuk el az ívet) szomszédtól.

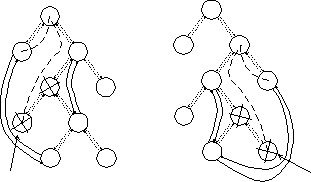
Befejezésül néhány szó a csúcsok és levelek tulajdonságairól. Különösképpen a parabolikus görbét ábrázoló fa és más struktúrák közti kapcsolat érdekel bennünket, illetve hogyan tárolodik a parabola a fában. Megjegyezzük, hogy nem egy valódi parabolát kell eltárolni hanem csak az azt definiáló pontot.Ezt a következő képlet adja

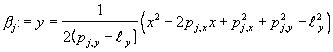
ahol jelenti a seprő egyenest a megfigylés pillanatában és jelenti azt a P-beli pontot, amely a ívet definiálja.
A bináris fa közbeeső csúcsai pointereket tartalmaznak a Voronoi diagram adatsruktúrájában meglévő élekhez. Igy minden Voronoi ponthoz tartozó él közvetlenül elérhető, amikor a kör esemény bekövetkezik, tehát nincs szükség a Voronoi diagram adastruktúrájában semmiféle keresési műveletre. A fa leveleiben egy kör eseményhez
mutat a pointer ha az ív kör eseményt definiál. Ha nem, a pointer NULL lesz. Ezt a pointert megtartva hamis esemény esetén sem kell keresést végrehajtanunk.

11. Az események tárolására szolgáló adastruktúra

A Q sor az események y oordinátája szerint van rendezve. Azokat az eseményeket tárolja, amelyek már ismertek. Pont esemény esetén a pont egyszerűen tárolva van. Kör esemény bekövetkeztekor a kör legutolso pontja tárolodik. Végül pedig egy pointer mutat a
a parabolikus görbe fájának azon leveléhez, amely az eltűnő ívet tárolja.